
 Properties of Energy & Matter
Properties of Energy & Matter
By J. C. Cranwell 10/06/98
Part VIII
Quantum Math
 When we differentiate, we get the instantaneous change in whatever equation or shape we consider.
When we differentiate, we get the instantaneous change in whatever equation or shape we consider.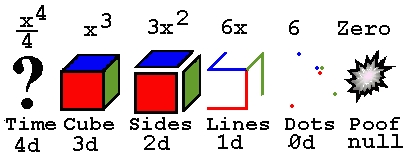 It's easy to visualize because the starting equation or figure, for instance a cube, gets lowered down a degree in power or dimension. A big problem occurs when we try to integrate something cubic ( third power ) into the fourth dimension ... what is it? Is it a snapshot in time? Is it an hypercube? Is it a mysterious visitor from the fourth dimension?
It's easy to visualize because the starting equation or figure, for instance a cube, gets lowered down a degree in power or dimension. A big problem occurs when we try to integrate something cubic ( third power ) into the fourth dimension ... what is it? Is it a snapshot in time? Is it an hypercube? Is it a mysterious visitor from the fourth dimension?
Particle Integration
 Remember, nothing is even remotely solid, so you will rack your brain trying to visualize the integration of a solid or in this case an actual
misconception. The mysterious 4-D shape is a tetrahedral axes shaped particle group of higher density. The basic unit of the x^3 variety is the X-Y-Z axes shaped particle. If in this example x = 1, then the three axis will be 1/3 in length
Remember, nothing is even remotely solid, so you will rack your brain trying to visualize the integration of a solid or in this case an actual
misconception. The mysterious 4-D shape is a tetrahedral axes shaped particle group of higher density. The basic unit of the x^3 variety is the X-Y-Z axes shaped particle. If in this example x = 1, then the three axis will be 1/3 in length 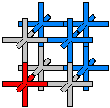 (X, Y and Z are 1/3 long) with a total length of one. All widths are infinitesimal. When we differentiate x^3 we get 3x^2 , this is 3 plus sign ( XY axes ) shaped particles with a total length of 3, that makes 6 axis with 1/2 length... this is also
(X, Y and Z are 1/3 long) with a total length of one. All widths are infinitesimal. When we differentiate x^3 we get 3x^2 , this is 3 plus sign ( XY axes ) shaped particles with a total length of 3, that makes 6 axis with 1/2 length... this is also  the exact amount of length needed to make three cubic particles... the XYZ's with 1/3 axis length, and the correct amount to add one particle either cubic (XYZ) or quadratic (XY) to every axis of the original differentiated particle giving the XYZ an instantaneous change.
So, working this in reverse we see that as we integrate into a higher power it changes the shape by adding an axis and it shrinks in size giving it a greater density. So the fourth Dimensional particle is composed of tetrahedral axes shapes,
the exact amount of length needed to make three cubic particles... the XYZ's with 1/3 axis length, and the correct amount to add one particle either cubic (XYZ) or quadratic (XY) to every axis of the original differentiated particle giving the XYZ an instantaneous change.
So, working this in reverse we see that as we integrate into a higher power it changes the shape by adding an axis and it shrinks in size giving it a greater density. So the fourth Dimensional particle is composed of tetrahedral axes shapes,  in this example 1/4 total length f (1) = x^4/4 = 1/4 with 1/16 length axis ( one fourth of total ), it gets small very rapidly. More particles are needed to fill any volume because of the shorter lengths and tighter pack, ergo higher density. Now it is easy to see... in a field of 2-D ( XY ) particles we can only traverse horizontally and vertically. When we bump this up one dimension into 3-D we also have the toward and away axis, alas we still can't move on a diagonal, for that is reserved for the higher dimensions. Now it's a piece of cake to see how any length, for instance 1/(10Ö26-1)c, divided up correctly can be a direct representation of a particle(s). If we replace the G in Newton's equation F = Gm1m2/r^2 with the exact value we get
F = m1m2 / ((10 Ö26-1)c)r^2 and can easily see the masses divided by the radius squared times the length in question equals the force of gravity.
Part IX
in this example 1/4 total length f (1) = x^4/4 = 1/4 with 1/16 length axis ( one fourth of total ), it gets small very rapidly. More particles are needed to fill any volume because of the shorter lengths and tighter pack, ergo higher density. Now it is easy to see... in a field of 2-D ( XY ) particles we can only traverse horizontally and vertically. When we bump this up one dimension into 3-D we also have the toward and away axis, alas we still can't move on a diagonal, for that is reserved for the higher dimensions. Now it's a piece of cake to see how any length, for instance 1/(10Ö26-1)c, divided up correctly can be a direct representation of a particle(s). If we replace the G in Newton's equation F = Gm1m2/r^2 with the exact value we get
F = m1m2 / ((10 Ö26-1)c)r^2 and can easily see the masses divided by the radius squared times the length in question equals the force of gravity.
Part IX
 Home Page
Home Page
 Goddess401
Goddess401

 Properties of Energy & Matter
Properties of Energy & Matter When we differentiate, we get the instantaneous change in whatever equation or shape we consider.
When we differentiate, we get the instantaneous change in whatever equation or shape we consider. It's easy to visualize because the starting equation or figure, for instance a cube, gets lowered down a degree in power or dimension. A big problem occurs when we try to integrate something cubic ( third power ) into the fourth dimension ... what is it? Is it a snapshot in time? Is it an hypercube? Is it a mysterious visitor from the fourth dimension?
It's easy to visualize because the starting equation or figure, for instance a cube, gets lowered down a degree in power or dimension. A big problem occurs when we try to integrate something cubic ( third power ) into the fourth dimension ... what is it? Is it a snapshot in time? Is it an hypercube? Is it a mysterious visitor from the fourth dimension?  Remember, nothing is even remotely solid, so you will rack your brain trying to visualize the integration of a solid or in this case an actual
misconception. The mysterious 4-D shape is a tetrahedral axes shaped particle group of higher density. The basic unit of the x^3 variety is the X-Y-Z axes shaped particle. If in this example x = 1, then the three axis will be 1/3 in length
Remember, nothing is even remotely solid, so you will rack your brain trying to visualize the integration of a solid or in this case an actual
misconception. The mysterious 4-D shape is a tetrahedral axes shaped particle group of higher density. The basic unit of the x^3 variety is the X-Y-Z axes shaped particle. If in this example x = 1, then the three axis will be 1/3 in length  (X, Y and Z are 1/3 long) with a total length of one. All widths are infinitesimal. When we differentiate x^3 we get 3x^2 , this is 3 plus sign ( XY axes ) shaped particles with a total length of 3, that makes 6 axis with 1/2 length... this is also
(X, Y and Z are 1/3 long) with a total length of one. All widths are infinitesimal. When we differentiate x^3 we get 3x^2 , this is 3 plus sign ( XY axes ) shaped particles with a total length of 3, that makes 6 axis with 1/2 length... this is also  the exact amount of length needed to make three cubic particles... the XYZ's with 1/3 axis length, and the correct amount to add one particle either cubic (XYZ) or quadratic (XY) to every axis of the original differentiated particle giving the XYZ an instantaneous change.
So, working this in reverse we see that as we integrate into a higher power it changes the shape by adding an axis and it shrinks in size giving it a greater density. So the fourth Dimensional particle is composed of tetrahedral axes shapes,
the exact amount of length needed to make three cubic particles... the XYZ's with 1/3 axis length, and the correct amount to add one particle either cubic (XYZ) or quadratic (XY) to every axis of the original differentiated particle giving the XYZ an instantaneous change.
So, working this in reverse we see that as we integrate into a higher power it changes the shape by adding an axis and it shrinks in size giving it a greater density. So the fourth Dimensional particle is composed of tetrahedral axes shapes,  in this example 1/4 total length f (1) = x^4/4 = 1/4 with 1/16 length axis ( one fourth of total ), it gets small very rapidly. More particles are needed to fill any volume because of the shorter lengths and tighter pack, ergo higher density. Now it is easy to see... in a field of 2-D ( XY ) particles we can only traverse horizontally and vertically. When we bump this up one dimension into 3-D we also have the toward and away axis, alas we still can't move on a diagonal, for that is reserved for the higher dimensions. Now it's a piece of cake to see how any length, for instance 1/(10Ö26-1)c, divided up correctly can be a direct representation of a particle(s). If we replace the G in Newton's equation F = Gm1m2/r^2 with the exact value we get
F = m1m2 / ((10 Ö26-1)c)r^2 and can easily see the masses divided by the radius squared times the length in question equals the force of gravity.
Part IX
in this example 1/4 total length f (1) = x^4/4 = 1/4 with 1/16 length axis ( one fourth of total ), it gets small very rapidly. More particles are needed to fill any volume because of the shorter lengths and tighter pack, ergo higher density. Now it is easy to see... in a field of 2-D ( XY ) particles we can only traverse horizontally and vertically. When we bump this up one dimension into 3-D we also have the toward and away axis, alas we still can't move on a diagonal, for that is reserved for the higher dimensions. Now it's a piece of cake to see how any length, for instance 1/(10Ö26-1)c, divided up correctly can be a direct representation of a particle(s). If we replace the G in Newton's equation F = Gm1m2/r^2 with the exact value we get
F = m1m2 / ((10 Ö26-1)c)r^2 and can easily see the masses divided by the radius squared times the length in question equals the force of gravity.
Part IX