That makes the volumetric or spatial difference one quadrillionth ( .000000000000001 ). This ratio is approximately the same size as a spherical dot above the letter " i " (the proton) on the fifty - yard line in a football stadium (the orbital) everything else is empty space. So if we think of or visualize a huge sphere the size of a stadium (a small moon for instance) in reality the amount of actual continuous mass (just nuclei)
| (4/3)Pi 13
---------------- |
= | 1
--------------------- |
= | one
quadrillionth |
Quantum Math
When we differentiate, we get
the instantaneous change in whatever equation or shape we consider. It's
easy to visualize because the starting equation or figure, for instance
a 3-dimensional cube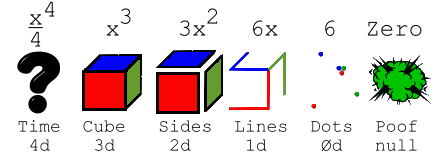 
we arrive at ( y'' = 6x ) this is simply six one dimensional lines or the
instantaneous change needed to increase the length and width (area) of
the three planes, every plane needs two lines (length and width) to increase
its area, three planes times two lines equals six lines total.
Now it gets
even easier ... six points ( y''' = 6 ) are the instantaneous change needed
to increase six lines in length (notice the six points are zero-dimensional).
Now we arrive at ( y (4 ) = 0 ) this is the instantaneous change
needed to take the six points out of existence.
A big problem occurs when we
try to integrate something cubic ( y = x3 ) into the fourth
dimension, in this case ( integral y ), we have an exact mathematical representation
of it ( x 4 /4 ) and if x = 1 we know this is equal to 1/4's
worth of fourth dimensional volume (tesserarea?) but, what shape is it?
Is it a snapshot in time? Is it an hypercube? Is it a mysterious visitor
from the fourth dimension?
The cube isn't solid
...Remember, nothing is
even remotely solid, so you will rack your brain trying to visualize the
integration of a solid or in this case an actual misconception. The
mysterious fourth dimensional shape is a tetrahedral axes shaped particle
group of higher density. Any one dimensional object is a line.
Any two
dimensional object is a plane, but that's a slice of a supposed cube, and
can't be thought of as for instance a sheet of paper because, if we integrate
enough of them into a stack, we have a solid cube of paper and by now we
know nothing is solid.
The cube can't be solid. So that form of thinking
is simply wrong (note: The one dimensional line would also have to be in
segments, and although we can actually integrate lines into a plane ...
the lines in this case are never arranged parallel so they won't form a
continuous plane that could then be integrated into a stack)...
The cube isn't solid but
since it is there, it must be made of something. If we call the basic unit
of whatever the cube is comprised of a particle. The particle must be capable
of conveying information, for instance electro - magnetic vibrations. And
since there are different frequencies and / or strengths of vibrations
with multiple simultaneous combinations, a zero-dimensional single point
particle would be incapable of achieving this. It can spin or move or remain
at rest but there is no chance of Simultaneity or vibrations. The next
possible alternative is the one dimensional line or string (any intrinsic
universal characteristic will always be the simplest and at the same time
most efficient option).
The string seems to be the shape of choice in this
case. On a musical instrument, a violin for instance, the string can convey
a multitude of vibrations, tones and harmonics. This means there can be
a lot of simultaneous information transmitted along a one dimensional string.
There is no need to attempt theoretical construction of a particle made
of two dimensional planes because ... if we integrate enough of them into
a stack...
Particle Integration
:
| x4/4 = 1/4
x3 = 1 3x2 = 3 6x = 6 |
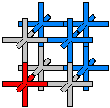this
is 3 plus signs or XY axes shaped particles with a total length of 3, that
makes 6 axis with 1/2 length... this is also the exact amount of length
needed to make three cubic particles... the XYZ's with 1/3 axis length,
and the correct amount to add one particle either cubic XYZ or quadratic
XY to every axis of the original differentiated particle giving the XYZ
an instantaneous change. 
So, working this in reverse we see that as we integrate into a higher power it changes the shape by adding an axis and it shrinks in size giving it a greater density. So the fourth dimensional object is composed of tetrahedral axes shapes, in this example 1/4 total length
Now it's a piece of cake to see how any length, for instance
Spatial dimension is directions.
An Abbott Flatlander from Flatland living on a two dimensional plane would actually be living on an infinity of dimensions
if
he can turn or move through every angle or vector direction on the supposed
plane. The way this actually works is by using axial directions as dimension.
An actual working two dimensional model of space would be an infinite array
of The actual
This axial concept allows for an actual visual of higher dimensions. If we integrate a supposed three-dimensional cube into the fourth dimension the result isn't a snapshot of the cube in the fourth dimension, it is a tetrahedron with an increased density field matrix (tetrahedral).
You have to remember... nothing is
If you want to bump up something in dimension until it is actually solid... you're on your way to creating your very own neutron star with a contiguous proton/neutron pack, We're all in trouble if we get a visit from one of them.
Quantum Weirdness:
Since everything involved
in the continuum structure is completely controlled or regulated at the
speed of light (including Stars, Planets, any type of measuring device,
Plants, Animals, Humans and everything else, excluding for instance neutrinos),
we have no way of knowing what speed things are really happening.
It's
like being a character in a movie, you're just film and you're trying to
find out what speed(s) the projector is running. The Speed of light and
all particle interactions might be traveling or happening at the pace of
an Escargot (snail) but our brains are using the same speed vibration set
by this cosmic speedometer so we'll never know.
| Properties of Energy & Matter | * part II * |
Goddess401
Home Page admin@gootar.com https://xulfrepus.neocities.org/